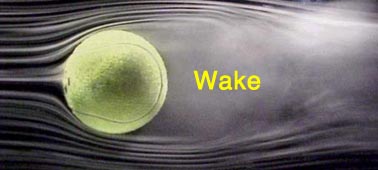
One of the most common questions that we received from folks during our Tennis Sport Science Project (wings.avkids.com/Tennis) was on the math and physical science governing the flight of tennis balls.

You know from experience the factors which govern a tennis ball's motion (speed, spin, height the ball is hit, etc.) but you may have wondered how to predict the effects on the ball's flight. Especially as discussions and questions arose with the introduction and testing of the larger Type 3 ball, you might have wanted to know exactly how the ball's diameter would affect the speed or impact point with the court. You even may have pulled out a high school or introductory college physics textbook only to find that those simplified trajectory equations you remembered didn't allow you to determine what would happen if the ball's diameter changed.

This is Trajectories 101A. Yes, this implies that there will be a 101B! This month we'll go through the basic trajectory science and next month finish off by putting the math together and some fun examples.

At this point, to make sure everyone has the same knowledge, we'll start with very basic definitions. You may wonder why we're discussing some of this right now but it all ties together in the end.

To model the flight of a tennis ball mathematically you need to determine what factors affect the ball's flight. Each of these factors in turn will have a mathematical expression that we'll use next time. For now and for this discussion we're going to limit ourselves to flight from the time the ball is struck to the instant before the first bounce. Let's just deal with serves right now.

What factors affect the flight of a tennis ball? Go ahead and jot them down. Your list might include: speed of the ball, angle of the racquet on impact with the ball, height at which the ball is struck, dwell time of the ball on the racquet, spin direction (topspin, underspin, slice), spin rate, environmental conditions (like wind on the court, altitude), ball size, type of ball (court specific, pressurized or pressureless), ball condition (new, used), I've actually played "Devil's Advocate" here. Some of these factors do affect the trajectory equations directly while others do not.

There's actually a method to solving all of these types of problems. You start by defining the forces that affect the situation. The term "forces" in physics and aerodynamics has a very specific meaning and very specific numerical units (like a newton) associated with it. Subsequently, the math equation for the forces around the tennis ball, is related to the equation for a balls' acceleration (rate of change of velocity), which in turn is related to equations for velocity and position on the court. So when we determine these forces, we'll have the key to solving the math for velocity along any point on the trajectory as well as where the ball will land.

The trajectory of a tennis ball flight is affected by three forces: the ball's weight, the drag (or retarding force caused by the air moving across the ball's fabric cover, against the ball's round shape and even by its spin) and lift. Lift is the force that pushes an airplane or a bird up against its weight and is created primarily by the movement of the air around the wings. The word "lift" is a little misleading, because one meaning of the word is "to rise." On an airplane normally (and thankfully) that means "up." But in aerodynamics lift has a very specific definition and is not always "up" as you'll see. On a tennis ball aerodynamic lift generally is created through spin. (The last segment of this article is devoted to spin and lift.) These three forces act in a "tug-of-war" or "arm-wrestle" between each other. The ball's path is the result of the combined strength and direction of these forces. Change one of these forces and the trajectory changes.

Lift and drag are both dependent on air density, velocity, and the ball's diameter. Additionally, lift is dependent on a coefficient of lift (C_l) and drag on a coefficient of drag (C_d).

C_l and C_d are numbers determined through wind tunnel or series of trajectory tests. C_d is affected by the object's surface roughness, shape and for some sports balls even the spin rate. C_l is affected by the ball's spin rate. C_l and C_d both change with velocity, so as the ball slows down from the time it is struck to the time it first hits the court, C_l and C_d may change values.

You may have already figured out some factors, like the weight of the ball, will directly "plug into" the trajectory math equations. Other factors, such as the altitude of the court, will be used to calculate one of the variables that will be plugged in. In this case, the altitude of the court affects the value of the air's density used in the lift and drag equations. Still other factors influence one of the variables, but are not used in the calculations. Dwell time on the racquet and racquet tension may affect the ball's speed, as would player biomechanics but only the ball's resulting velocity is plugged into the trajectory equations regardless of how that velocity was generated. Finally, some factors will have no influence on the math equations at all - once the ball is set in motion whether a ball is pressurized or pressureless will not affect the trajectory equations as long as the balls' weight, lift and drag are the same. So when we "do the math" next month, we'll be separating out the items in our list that plug right into the math, versus the ones that "influence" one of these factors.

I wanted to share one final aspect of ball trajectories. Maybe you've wondered why a topspin ball drops faster than a ball with underspin?

Here are some photos from a wind tunnel test conducted with my colleague Dr. Rabi Mehta from the NASA Ames Research Center. Wind tunnels are used to visually study the flow over the ball as well as to determine the numerical values of the lift and drag coefficients. This tunnel (and in general most wind tunnels) is not used to observe a ball's trajectory.

In Figure 1, the tennis ball is not spinning. The ball is stationary while the smoke is moving from left to right, simulating a ball moving from right to left. Early aerodynamicists recognized it didn't matter if an object moved through a fluid (a liquid or a gas) at a certain speed or the object was held stationary and the fluid moved over the a stationary object at that same speed - the forces would be the same. Clearly, wind tunnel testing makes determining whether or not an object like a new aircraft wing design will have enough lift much simpler and safer than just building the wing and flying it on the aircraft.

Figure 1 - No Spin

There is a lot of information that can be determined just from studying videos of the tunnel tests and still photos. You can see that the flow over the top of the ball looks just about like a mirror image (symmetrical) to the flow across the bottom of the ball. You can see that the smoke and air follow the contour of the ball until the smoke reaches the right side of the ball. Then the airflow isn't able to negotiate the turn around the backside of the ball. The airflow has really separated from the ball. So although the top and bottom halves of the photo look the same, the right and left sides of the photo do not. That empty voided looking area on the right hand side of the photo behind the ball, in the middle of the picture is the wake. The wake is an indication of how much drag there is. For comparison, Figure 2 is a bowling ball -- much, much smoother than the tennis ball nap cover. You can see on the bowling ball that the wake on the right hand side is much smaller. There is a lot less drag force on the bowling ball.

Figure 2 - Bowling Ball

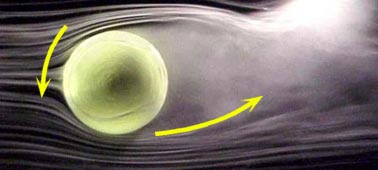
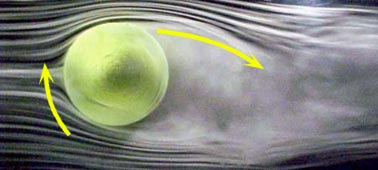
Now let's examine spinning balls. Figure 3 is a ball with topspin and Figure 4 is a ball with underspin. What's different? Let's start with Figure 3 (topspin). The top and bottom halves of the photo no longer look identical. On the right side of the topspin ball photo the wake is tilted up. The airflow behind the topspin ball is being forced upwards. Compare this with Figure 4 (underspin) where the wake is pointed down.

Figure 3 - Topspin

Figure 4 - Underspin

Okay - but in topspin the ball drops faster. Why is the wake tilted up for topspin - wouldn't that mean that topspin ball is being pushed up and not dropping faster? The direction of the wakes might be a little puzzling at first. Now we need to remember Newton's Third Law Of Motion: "For every action there is an equal and opposite reaction." The fact that the wake is pointed upwards signifies that the ball is actually being forced down. For underspin the opposite is true - the wake pointing down signifies that the ball is being forced up. If instead of a ball you held a pen in your hand and pushed the right side of the pen up, which direction would the left side of the pen point? It would point down. The same thing basically happens on the ball, the airflow pushes the right side of the ball up, pushing the left side of the ball moving along the flight path down.

That's all for Trajectories 101A for now. Hope you will visit the Tennis SET column next month for the conclusion. We'll specifically go through the math equations that take you from forces to the location on the court. We'll do a flight comparison for the US Open in New York (located at about sea level) versus a ball under all the same conditions at the imaginary "Mount Everest Open" located at 29,000 feet or 8800 meters above sea level. (You'll see curving a ball with spin is much more difficult at higher altitudes.)

Don't hesitate to write me using this form if you have questions.

Wishing You A Healthy And Prosperous New Year!